1. 进制介绍
进制介绍
进制就是进位制,是人们规定的一种进位方法。 对于任何一种进制—X进制,就表示某一位置上的数运算时是逢X进一位,二进制就是逢二进一,八进制是逢八进一,十进制是逢十进一,十六进制是逢十六进一。
Java进制分为二进制,八进制,十进制,十六进制, 但是计算机只能处理2进制的数据和指令。
- 对于整数, 有四种表示方式:
| 进制 | 组成 | 规则 | 开头 |
|---|---|---|---|
| 二进制 | 0,1 | 满 2 进 1 | 0b 或 0B 开头 |
| 八进制 | 0-7 | 满 8 进 1 | 0 开头 |
| 十进制 | 0-9 | 满 10 进 1 | |
| 十六进制 | 0-9 A(10), B(11), C(12), D(13), E(14), F(15) | 满 16 进 1 | 以 0x 或 0X 开头 |
- 进制对照表
| 二进制 | 八进制 | 十进制 | 十六进制 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 10 | 2 | 2 | 2 |
| 11 | 3 | 3 | 3 |
| 100 | 4 | 4 | 4 |
| 101 | 5 | 5 | 5 |
| 110 | 6 | 6 | 6 |
| 111 | 7 | 7 | 7 |
| 1000 | 10 | 8 | 8 |
| 1001 | 11 | 9 | 9 |
| 1010 | 12 | 10 | A |
| 1011 | 13 | 11 | B |
| 1100 | 14 | 12 | C |
| 1101 | 15 | 13 | D |
| 1110 | 16 | 14 | E |
| 1111 | 17 | 15 | F |
| 10000 | 20 | 16 | 10 |
| 10001 | 21 | 17 | 11 |
- 在代码中定义各种进制
public class BinaryTest {
public static void main(String[] args) {
// 二进制
int i1 = 0b1010;
System.out.println("i1 = "+i1); // i1 = 10
// 八进制
int i2 = 01354;
System.out.println("i2 = "+i2); // i2 = 748
// 十进制
int i3 = 1234;
System.out.println("i3 = "+i3); // i3 = 1234
// 十六进制
int i4 = 0X7B8F;
System.out.println("i4 = "+i4); // i4 = 31631
}
}2. 进制的转换
2.1 十进制转二进制
- 规则
将十进制数除以 2, 直到最后商为 0 为止, 然后将最后一步得到的结果与之前每个步骤得到的余数倒过来, 就是对应的二进制数
- 示例
将十进制数 35 转成对应的二进制数结果为 0B100011 计算过程如下图所示:

- 验证
// 十进制转二进制
System.out.println(Integer.toBinaryString(35)); // 1000112.2 十进制转八进制
- 规则
将十进制数除以 8, 直到最后商为 0 为止, 然后将最后一步得到的结果与之前每个步骤得到的余数倒过来, 就是对应的二进制数
- 示例
将十进制数 156 转成八进制数为 0234 计算过程如下图所示:
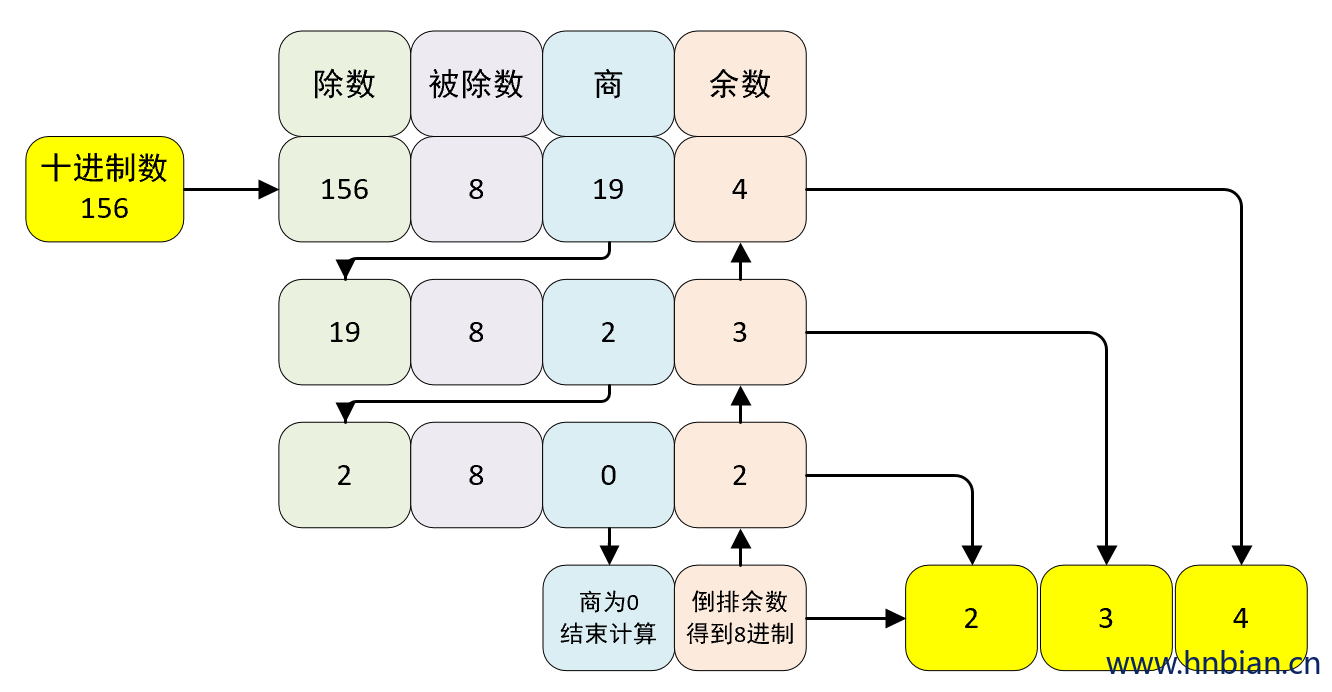
- 验证
// 十进制转八进制
System.out.println(Integer.toOctalString(156)); // 2342.3 十进制转十六进制
- 规则
将十进制数除以 16, 直到最后商为 0 为止, 然后将最后一步得到的结果与之前每个步骤得到的余数倒过来, 就是对应的二进制数
- 示例
将十进制数 2021转成 十六 进制数为 7E5 计算过程如下图所示:
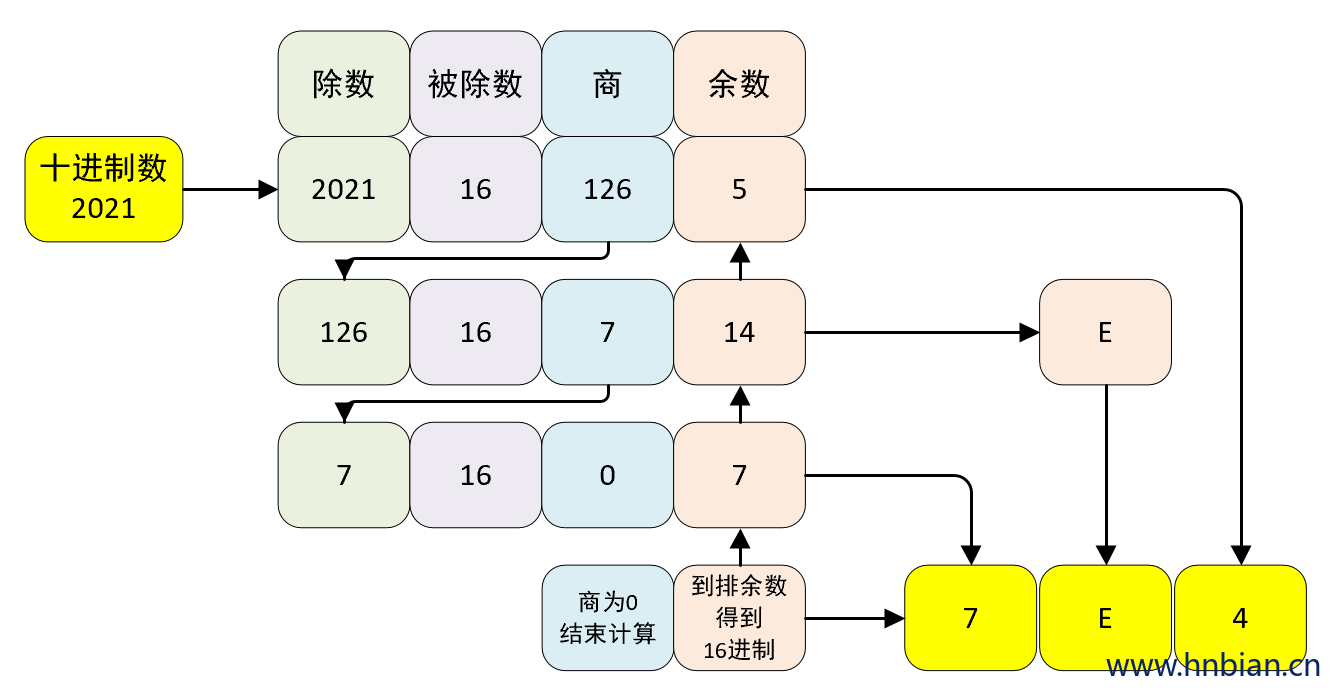
- 验证
// 十进制转十六进制
System.out.println(Integer.toHexString(2021)); // 7e52.4 二进制转十进制
计算规则
从最右侧开始, 将每个位上的数提出来, 乘以 2 的 (位数-1) 次方, 然后将这些数求和
示例
将二进制数 0B1011 转成十进制数为 11 计算过程如下表格所示:
| 位数 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|
| 二进制数 | 1 | 0 | 1 | 1 |
| 逐位计算 | $1(2^{(4-1)})$ | $0(2^{(3-1)})$ | $1(2^{(2-1)})$ | $1(2^{(1-1)})$ |
| 简化幂数 | $1(2^3)$ | $0(2^2)$ | $1(2^1)$ | $1(2^0)$ |
| 简化算式 | 1*8 | 0*4 | 1*2 | 1*1 |
| 逐位结果 | 8 | 0 | 2 | 1 |
| 最终结果 | 8+0+2+1 = 11 |
- 验证
// 二进制转十进制
System.out.println(0B1011); // 112.5 八进制转十进制
计算规则
从最右侧开始, 将每个位上的数提出来, 乘以 8 的 (位数-1) 次方, 然后将这些数求和
示例
将八进制数 01034 转成十进制为 540 计算过程如下表格所示:
| 位数 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|
| 八进制数 | 1 | 0 | 3 | 4 |
| 逐位计算 | $1(8^{(4-1)})$ | $0(8^{(3-1)})$ | $3(8^{(2-1)})$ | $4(8^{(1-1)})$ |
| 简化幂数 | $1(8^{3})$ | $0(8^{2})$ | $3(8^{1})$ | $4(8^{0})$ |
| 简化算式 | 1*512 | 0*64 | 3*8 | 4*1 |
| 逐位结果 | 512 | 0 | 24 | 4 |
| 最终结果 | 512+0+24+4 = 540 |
- 验证
// 八进制转十进制 System.out.println(01034); // 540
2.6 十六进制转十进制
计算规则
从最右侧开始, 将每个位上的数提出来, 乘以 16 的 (位数-1) 次方, 然后将这些数求和.
示例
将十六进制数 0XA1F9 转成十进制数为 41465 计算过程如下表格所示:
| 位数 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|
| 十六进制数 | A | 1 | F | 9 |
| 对应十进制 | 10 | 1 | 15 | 9 |
| 逐位计算 | $10(16^{(4-1)})$ | $1(16^{(3-1)})$ | $15(16^{(2-1)})$ | $916^{(1-1)})$ |
| 简化幂数 | $10(16^{3})$ | $1(16^{2})$ | $1516^{1})$ | $9(16^{0})$ |
| 简化算式 | 10*4096 | 1*256 | 15*16 | 9*1 |
| 逐位结果 | 40960 | 256 | 240 | 9 |
| 最终结果 | 40960+256+240+9= 41465 |
- 验证
// 十六进制转十进制
System.out.println(0XA1F9); // 414652.7 二进制转八进制
- 规则
从低位开始, 将二进制数的每三个位为一组, 转成对应的十进制数, 然后将所有数拼接, 即为二进制对应的八进制
- 示例
将二进制数 0B1011010111 转成八进制为 01327
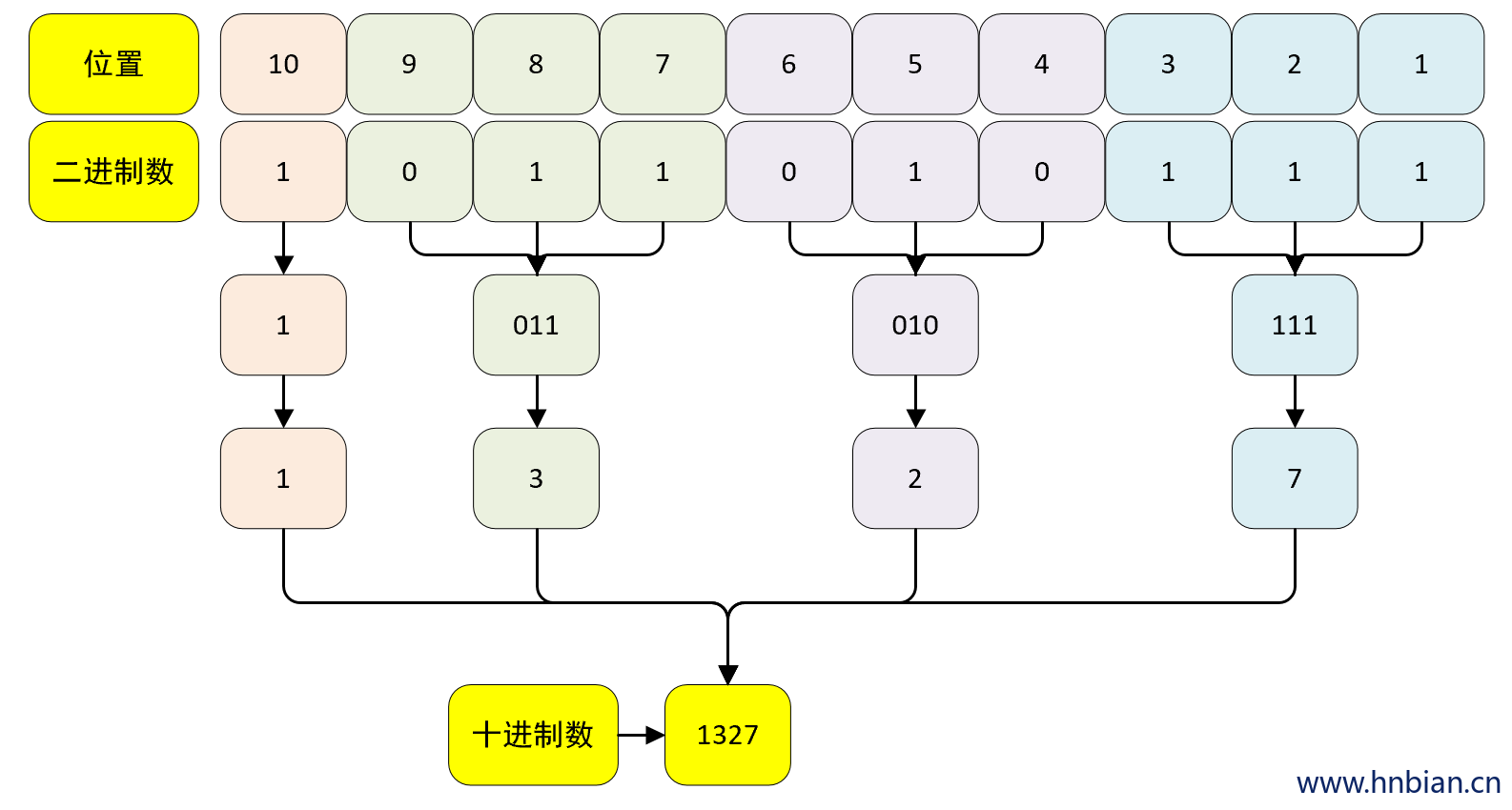
- 验证
// 二进制转八进制
System.out.println(Integer.toOctalString(0B1011010111)); // 013272.8 二进制转十六进制
- 规则
从低位开始, 将二进制数的每四个位为一组, 转成对应的十进制数, 然后将所有数拼接, 即为二进制对应的八进制
- 示例
将二进制数 0B1011010111 转成十六进制数为 0X2D7 , 计算过程如下图所示:
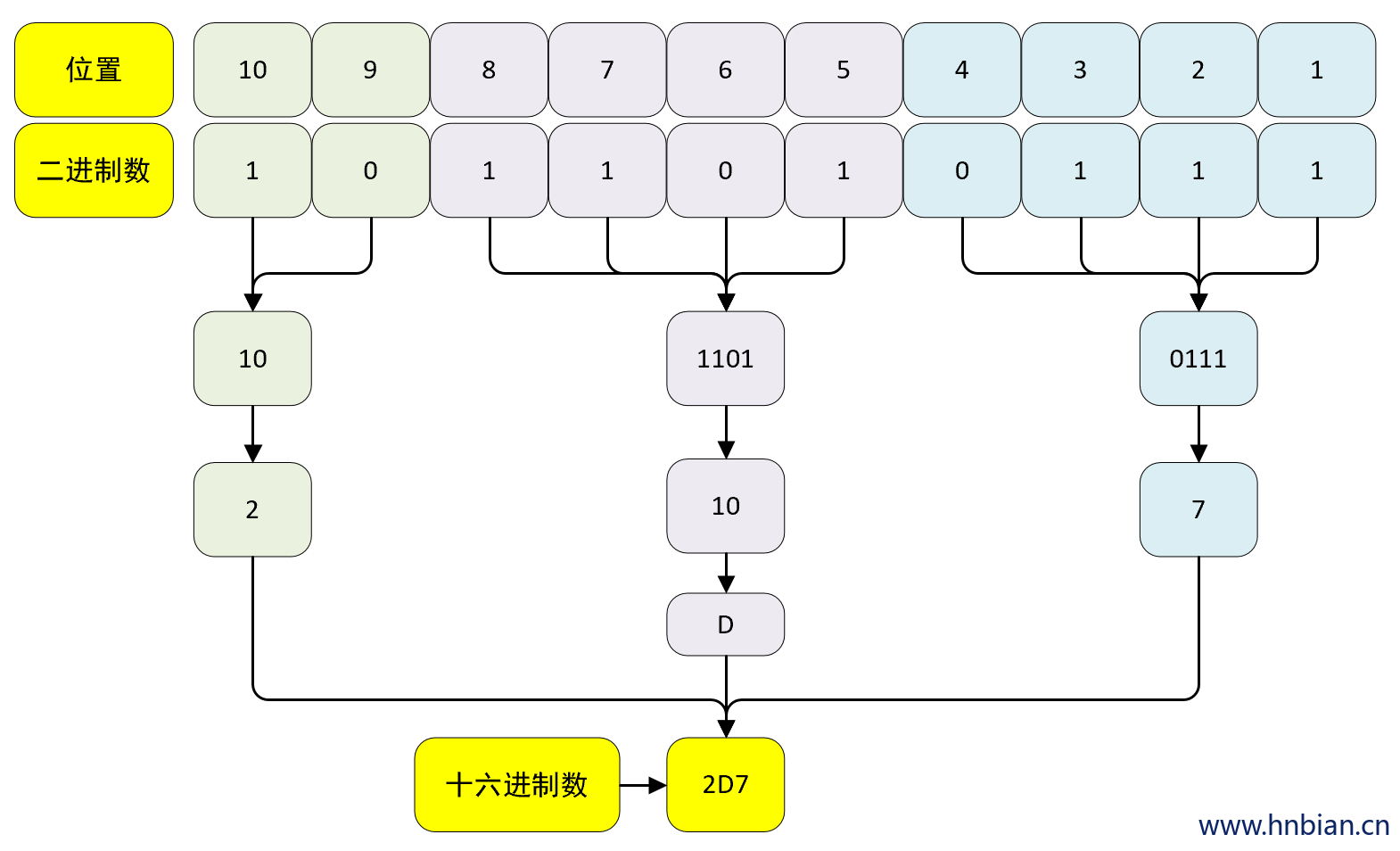
- 验证
// 二进制转十六进制
System.out.println(Integer.toHexString(0B1011010111)); // 2d72.9 八进制转二进制
- 规则:
将八进制的每一位转成对应的三位二进制数,然后将所有二进制数拼接, 即为对应的二进制数值
- 示例
将八进制数 0673 转成二进制数为 0B 1 1011 1011 , 计算过程如下图所示:
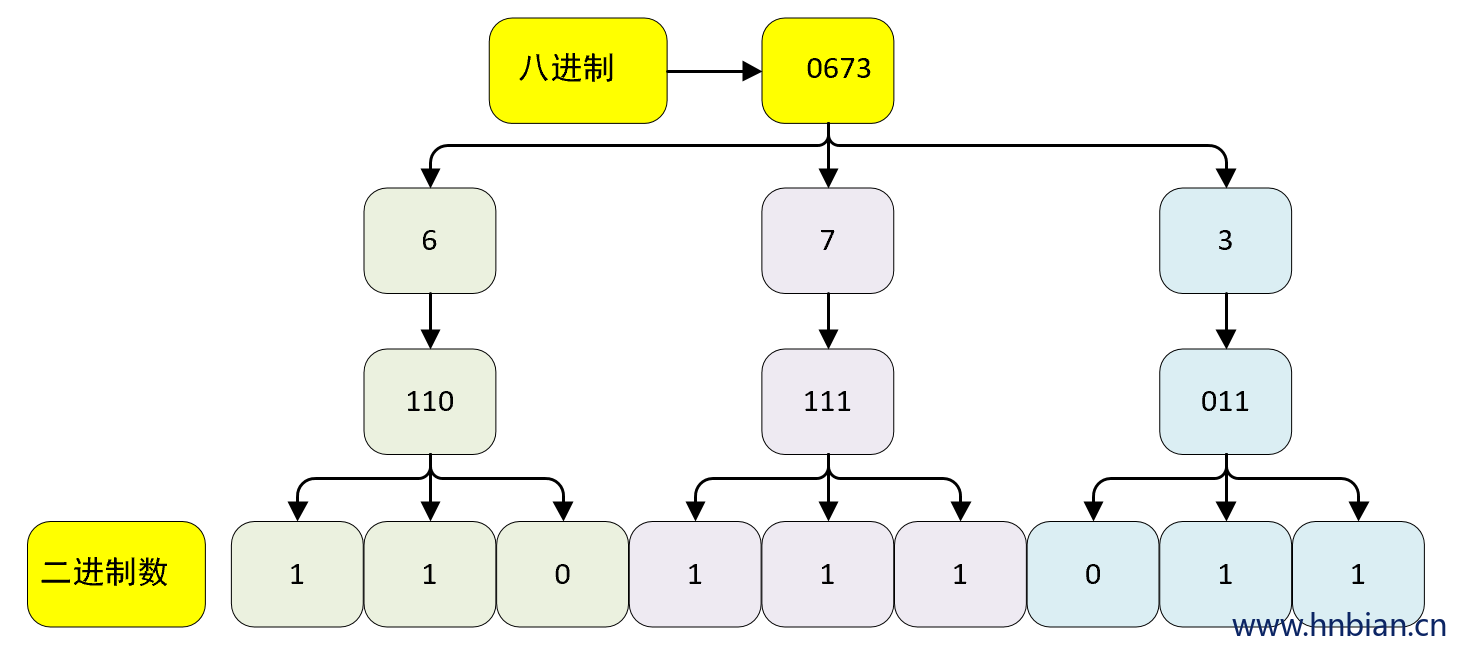
- 验证
// 八进制转二进制
System.out.println(Integer.toBinaryString(0673)); // 1101110112.10 十六进制转二进制
- 规则:
将八进制的每一位转成对应的四位二进制数,然后将所有二进制数拼接, 即为对应的二进制数值
- 示例
将十六进制数 0X9FA6 转成二进制数结果为 0B 1001 1111 1010 0110, 计算过程如下图所示:
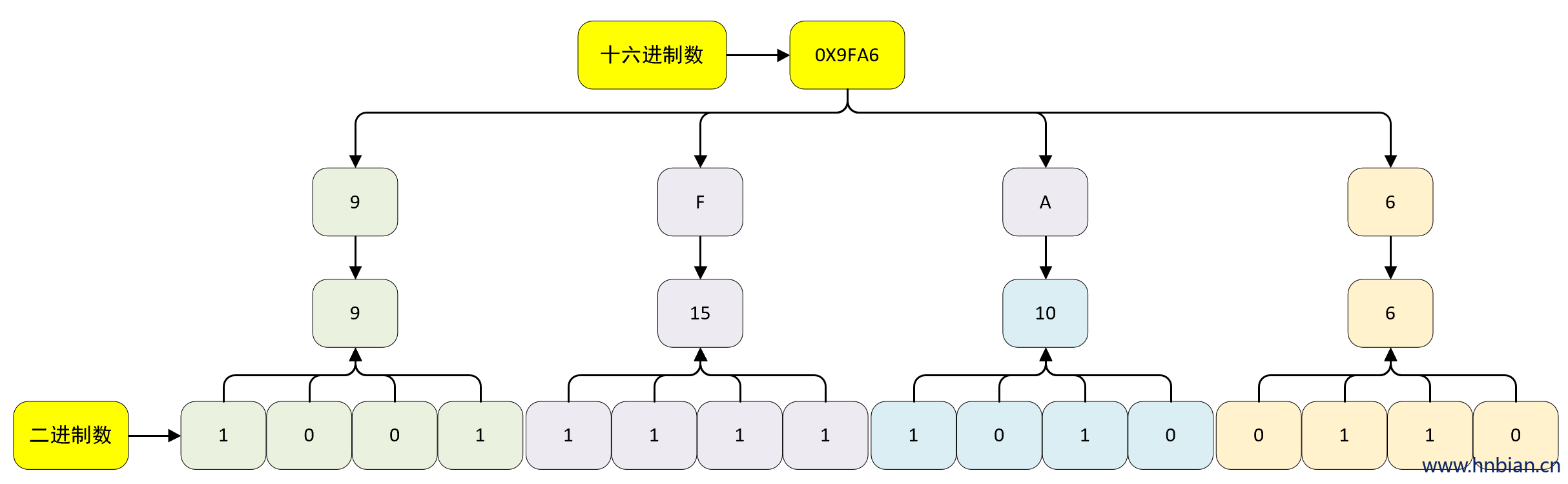
- 验证
// 十六进制转二进制
System.out.println(Integer.toBinaryString(0X9FA6)); // 10011111101001103. 位运算
位运算时程序设计中的对二进制数进行的操作, 通常位运算比加减法略快, 但比乘除法运算要快很多, Java 支持 7 种位运算, 一般来说位运算只能操作整数类型的值或变量.
3.1 位运算符介绍
| 符号 | 名称 | 运算规则 | 规律 |
|---|---|---|---|
| & | 按位与 | 符号两侧全为 1, 结果为 1, 否则为0 | |
| | | 按位或 | 符号两侧只要有一个为 1, 结果就为 1 (两侧全 0, 才为 0) | |
| ^ | 按位异或 | 符号两侧一样为 0,不一样为 1 | |
| ~ | 按位取反 (单目操作) |
0 变 1, 1 变 0 | |
| << | 算术左移 | 将操作数的二进制码整体左移指定位数,左移后右边空出来的位以0填充 | |
| >> | 算术右移 | 把第一个操作数的二进制码右移指定位数 左边空出来的位以原来的符号位填充,即: 如果第一个操作数原来是正数,则左边补0; 如果第一个操作数原来是负数,则左边补1。 |
|
| >>> | 无符号右移 | 把第一个操作数的二进制码右移指定位数,左边空出来的位总是以0填充。 |
| a | b | a&b | a|b | a^b | ~a |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 |
3.2 原码、反码与补码
原码,反码,补码
- 二进制的最高位是符号位, 0 表示正数, 1 表示负数
- 正数的 原码, 反码, 补码 都一样
- 负数的 反码 = 原码的符号位不变,其他位取反
- 负数的 补码 = 反码 + 1
- 负数的 反码 = 补码 - 1
- 0 的 反码, 补码 都是 0
- Java 中的数都是有符号位的,没有无符号数
- 在计算机进行运算的时候, 都是以 补码 方式进行运算的,因为补码可以将正负数统一
- 当我们看结果的时候要看 原码
3.3 取反运算
- 按位取反只需要一个操作数,
- 按位取反将将操作数的二进制码包括符号位按位取反.
- 操作符: ~
- 结果规律: $~X = -X-1$
public class BitwiseNot {
public static void main(String[] args) {
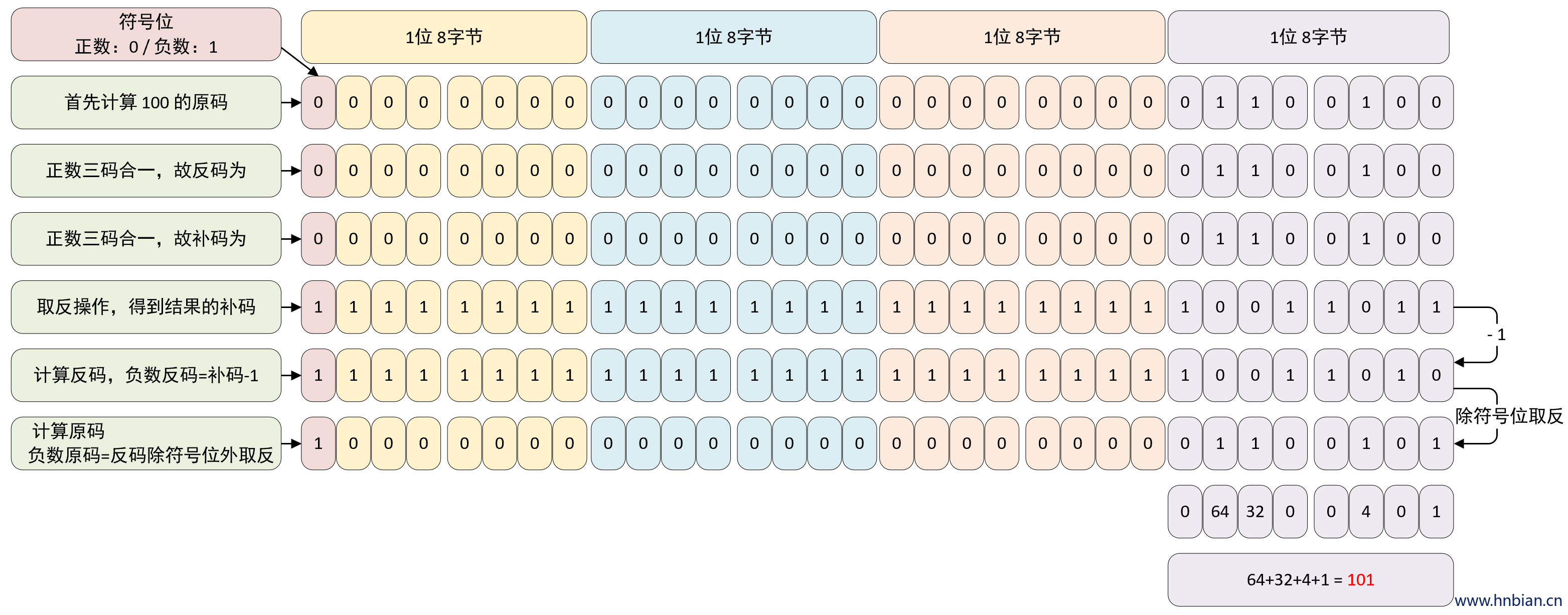
// 1. 计算 ~100
System.out.println("~100 = " + (~100)); // ~100 = -101
/**
* 解析
* 先得到 100 的源码 (正数 三码合一, 所以源码即反码即补码)
* 100 的源码为: 0000-0000 0000-0000 0000-0000 0110-0100
*
* 操作数的补码 -> 0000-0000 0000-0000 0000-0000 0110-0100 (执行取反运算 得到结果的补码)
* 结果数的补码 -> 1111-1111 1111-1111 1111-1111 1001-1011 (负数补码-1为反码 得到结果的反码)
* 结果数的反码 -> 1111-1111 1111-1111 1111-1111 1001-1010 (负数反码除符号位,其余取反得到结果的原码)
* 结果数的原码 -> 1000-0000 0000-0000 0000-0000 0110-0101 = > -101
*/
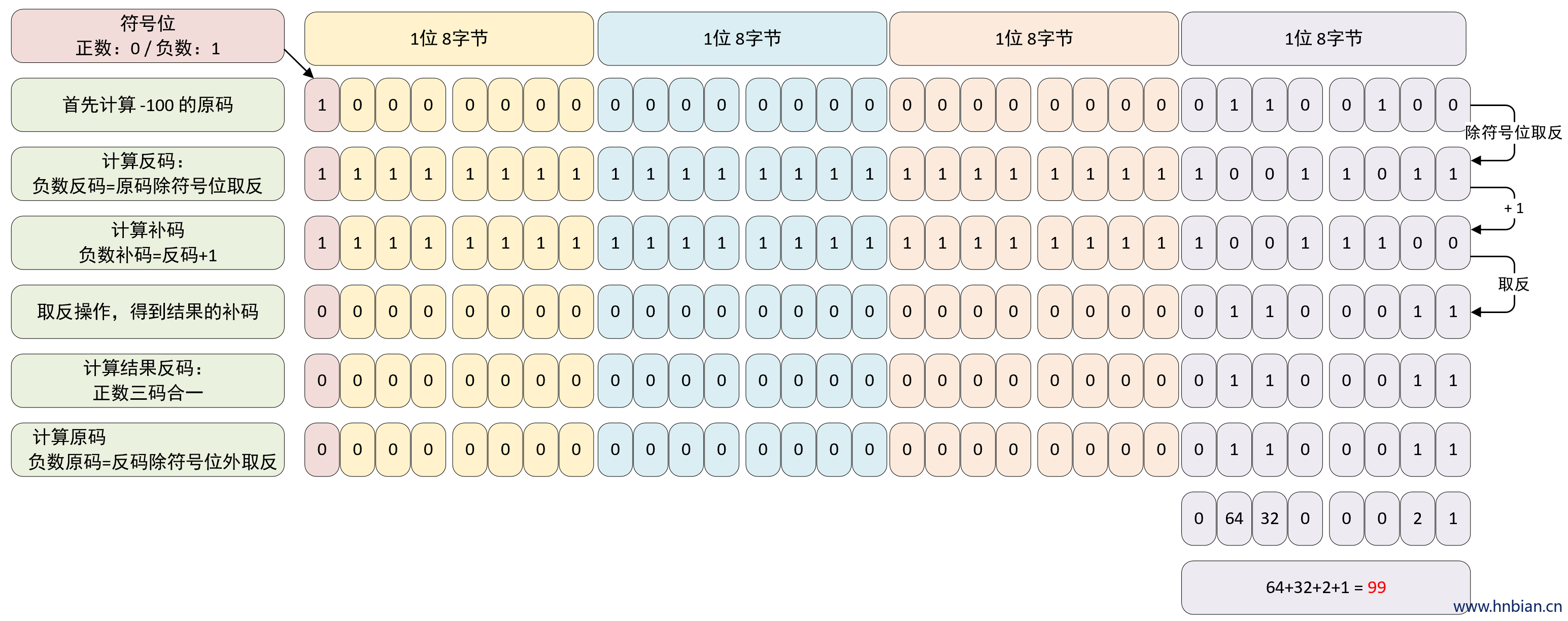
// 2. 计算 ~-100
System.out.println("~-100 = " + (~-100)); // ~-100 = 99
/**
* 解析
*
* 操作数的源码 -> 1000-0000 0000-0000 0000-0000 0110-0100 (得到反码, 除符号位所有位取反)
* 操作数的反码 -> 1111-1111 1111-1111 1111-1111 1001-1011 (得到操作数补码, 反码+1 = 补码)
* 操作数的补码 -> 1111-1111 1111-1111 1111-1111 1001-1100 (计算结果的补码,全部取反操作)
* 结果数的补码 -> 0000-0000 0000-0000 0000-0000 0110-0011 (结果为正数,三码合一, 所以这就是结果 99)
*/
System.out.println("~1000 = " + (~1000)); // ~1000 = -1001
System.out.println("~-1000 = " + (~-1000)); // ~-1000 = 999
System.out.println("~-569 = " + (~-569)); // ~-569 = 568
System.out.println("~-579 = " + (~-579)); // ~-579 = 578
System.out.println("~579 = " + (~579)); // ~579 = -580
}
}
3.4 按位与运算
按位与处理两个长度相同的二进制数,两个相应的二进位都为1,该位的结果值才为1,否则为0
- 操作符: &
public class BitwiseAnd {
public static void main(String[] args) {
// 1. 计算 7 & 4
System.out.println("7 & 4 = " + (7 & 4)); // 7 & 4 = 4
/*
7 跟 4 都是正数, 均为 3 码合一
得到 7 的原码 0000-0000 0000-0000 0000-0000 0000-0111
得到 4 的原码 0000-0000 0000-0000 0000-0000 0000-0100
进行按位与运算----------------------------------------
得到结果 0000-0000 0000-0000 0000-0000 0000-0100
所以结果为 4
*/
// 2. 计算 -3 & 6
System.out.println("-3 & 6 = " + (-3 & 6)); // -3 & 6 = 4
/*
解析
负数的补码 = 反码 +1
负数的反码 = 补码 -1
1.
获得-3 的原码 1000-0000 0000-0000 0000-0000 0000-0011
获得-3 的反码 1111-1111 1111-1111 1111-1111 1111-1100
获得-3 的补码 1111-1111 1111-1111 1111-1111 1111-1101 (负数补码等于反码+1)
获得 6 的补码 0000-0000 0000-0000 0000-0000 0000-0110 (正数三码合一原码即补码)
1111-1111 1111-1111 1111-1111 1111-1101 (-3 的补码)
按位与 & 0000-0000 0000-0000 0000-0000 0000-0110 ( 6 的补码)
----------------------------------------------------
结果 0000-0000 0000-0000 0000-0000 0000-0100 (补码)
结果为正数 三码合一, 所以结果为 4
*/
// 3. 计算 -9 & -7
System.out.println("-9 & -7 = " + (-9 & -7)); // -9 & -7 = -15
/*
解析
负数的补码 = 反码 +1
负数的反码 = 补码 -1
负数的反码 = 原码除符号位取反
1. 得到 -9 的补码
-9 原码为: 1000-0000 0000-0000 0000-0000 0000-1001
-9 反码为: 1111-1111 1111-1111 1111-1111 1111-0110
-9 的补码: 1111-1111 1111-1111 1111-1111 1111-0111
2. 得到-7 的补码
-7 原码为: 1000-0000 0000-0000 0000-0000 0000-0111
-7 反码为: 1111-1111 1111-1111 1111-1111 1111-1000
-7 补码为: 1111-1111 1111-1111 1111-1111 1111-1001
3. 进行按位与运算
1111-1111 1111-1111 1111-1111 1111-0111 (-9 的补码)
& 1111-1111 1111-1111 1111-1111 1111-1001 (-7 的补码)
--------------------------------------------
结果的补码 1111-1111 1111-1111 1111-1111 1111-0001
转结果反码 1111-1111 1111-1111 1111-1111 1111-0000
转结果原码 1000-0000 0000-0000 0000-0000 0000-1111
所以结果为 -15
*/
}
}

3.5 按位或运算
按位或处理两个长度相同的二进制数,两个相应的二进位中只要有一个为1,该位的结果值为1
- 操作符: |
public class BitwiseOr {
public static void main(String[] args) {
// 1. 计算 8|5
System.out.println("8|5 = "+(8|5)); // 8|5 = 13
/*
8 跟 5 都是正数, 均为 3 码合一
得到 8 的原码 0000-0000 0000-0000 0000-0000 0000-1000(正数 原码=反码=补码)
得到 5 的原码 0000-0000 0000-0000 0000-0000 0000-0101(正数 原码=反码=补码)
进行按位与运算----------------------------------------
得到结果 0000-0000 0000-0000 0000-0000 0000-1101
所以结果为 13
*/
// 2. 计算 7|-6
System.out.println("7|-6 = "+(7|-6)); // 7|-6 = -1
/*
解析
负数的补码 = 反码 +1
负数的反码 = 补码 -1
1.
获得-6 的原码 1000-0000 0000-0000 0000-0000 0000-0110
获得-6 的反码 1111-1111 1111-1111 1111-1111 1111-1001
获得-6 的补码 1111-1111 1111-1111 1111-1111 1111-1010 (负数补码等于反码+1)
获得 7 的原码 0000-0000 0000-0000 0000-0000 0000-0111 (正数 原码=反码=补码)
1111-1111 1111-1111 1111-1111 1111-1010 (-6 的补码)
按位或 | 0000-0000 0000-0000 0000-0000 0000-0111 ( 7 的补码)
----------------------------------------------------
得到结果的补码 1111-1111 1111-1111 1111-1111 1111-1111
得到结果的反码 1111-1111 1111-1111 1111-1111 1111-1110
得到结果的原码 1000-0000 0000-0000 0000-0000 0000-0001
所以结果为 -1
*/
// 3. 计算 -5|-3
System.out.println("-5|-3 = "+(-5|-3)); // 7|-6 = -1
/*
解析
负数的补码 = 反码 +1
负数的反码 = 补码 -1
负数的反码 = 原码除符号位取反
1. 得到 -5 的补码
-5 原码为: 1000-0000 0000-0000 0000-0000 0000-0101
-5 反码为: 1111-1111 1111-1111 1111-1111 1111-1010
-5 的补码: 1111-1111 1111-1111 1111-1111 1111-1011
2. 得到-3 的补码
-3 原码为: 1000-0000 0000-0000 0000-0000 0000-0011
-3 反码为: 1111-1111 1111-1111 1111-1111 1111-1100
-3 补码为: 1111-1111 1111-1111 1111-1111 1111-1101
3. 进行按位与运算
1111-1111 1111-1111 1111-1111 1111-1011 (-5 的补码)
& 1111-1111 1111-1111 1111-1111 1111-1101 (-3 的补码)
--------------------------------------------
结果的补码 1111-1111 1111-1111 1111-1111 1111-1111
转结果反码 1111-1111 1111-1111 1111-1111 1111-1110
转结果原码 1000-0000 0000-0000 0000-0000 0000-0001
所以结果为 -1
*/
}
}3.6 按位异或运算
- 按位异或运算,操作的结果是如果不同则该位为1,相同否则该位为0
- 操作符: ^
- 说明:
- 任何数与 0 做异或操作,结果都为其本身
- 任何数与本身做异或操作,结果都为 0
public class BitwiseXor {
public static void main(String[] args) {
// 1. 计算 8^5
System.out.println("8^5 = "+(8^5)); // 8^5 = 13
/*
8 跟 5 都是正数, 均为 3 码合一
得到 8 的原码 0000-0000 0000-0000 0000-0000 0000-1000
得到 5 的原码 0000-0000 0000-0000 0000-0000 0000-0101
按位异或运算------------------------------------------
得到结果补码 0000-0000 0000-0000 0000-0000 0000-1101
所以结果为 13
*/
// 2. 计算 7^-6
System.out.println("7^-6 = "+(7^-6)); // 7^-6 = -3
/*
解析
负数的补码 = 反码 +1
负数的反码 = 补码 -1
1.
获得-6 的原码 1000-0000 0000-0000 0000-0000 0000-0110
获得-6 的反码 1111-1111 1111-1111 1111-1111 1111-1001
获得-6 的补码 1111-1111 1111-1111 1111-1111 1111-1010 (负数补码等于反码+1)
获得 7 的原码 0000-0000 0000-0000 0000-0000 0000-0111
1111-1111 1111-1111 1111-1111 1111-1010 (-6 的补码)
按位异或 ^ 0000-0000 0000-0000 0000-0000 0000-0111 ( 7 的补码)
----------------------------------------------------
得到结果的补码 1111-1111 1111-1111 1111-1111 1111-1101
得到结果的反码 1111-1111 1111-1111 1111-1111 1111-1100
得到结果的原码 1000-0000 0000-0000 0000-0000 0000-0011
所以结果为 -3
*/
// 3. 计算 -5^-3
System.out.println("-5^-3 = "+(-5^-3)); // -5^-3 = 6
/*
解析
负数的补码 = 反码 +1
负数的反码 = 补码 -1
负数的反码 = 原码除符号位取反
1. 得到 -5 的补码
-5 原码为: 1000-0000 0000-0000 0000-0000 0000-0101
-5 反码为: 1111-1111 1111-1111 1111-1111 1111-1010
-5 的补码: 1111-1111 1111-1111 1111-1111 1111-1011
2. 得到-3 的补码
-3 原码为: 1000-0000 0000-0000 0000-0000 0000-0011
-3 反码为: 1111-1111 1111-1111 1111-1111 1111-1100
-3 补码为: 1111-1111 1111-1111 1111-1111 1111-1101
3. 进行按位异或运算
1111-1111 1111-1111 1111-1111 1111-1011 (-5 的补码)
^ 1111-1111 1111-1111 1111-1111 1111-1101 (-3 的补码)
--------------------------------------------
结果的补码 0000-0000 0000-0000 0000-0000 0000-0110
正数三码合一,所以结果为 6
*/
}
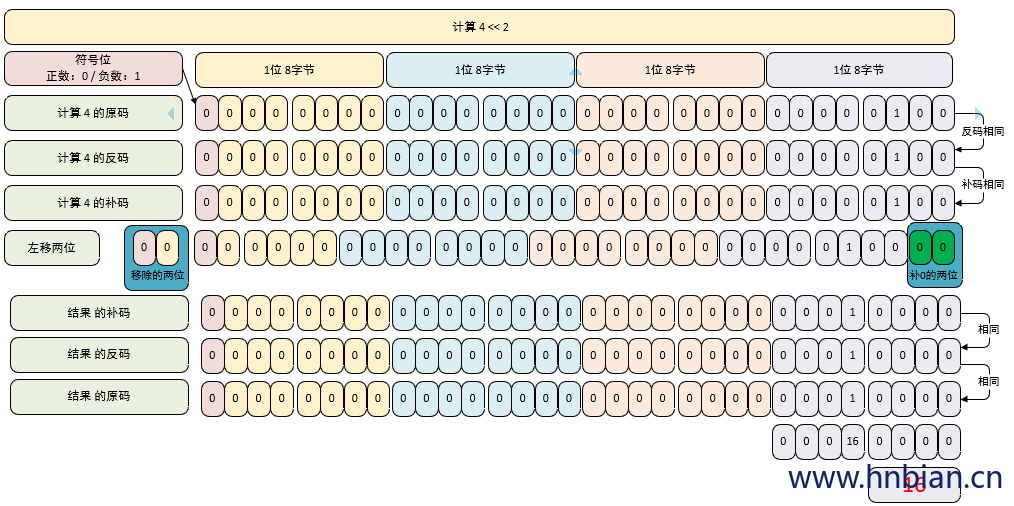
}3.7 算术左移运算
- 算术左移是将二进制数整体左移指定位数
- 左移后空出来的位用 0 补充
- 操作符: <<
- 规律 $x << n = x * ( 2^n )$
public class BitwiseLeft {
public static void main(String[] args) {
// 1. 计算 4 << 2
System.out.println("4 << 2 = "+(4 << 2));
// = 4* (2^2) = 16
/*
得到 4 的补码 0000-0000 0000-0000 0000-0000 0000-0100
左移两位 00-0000 0000-0000 0000-0000 0000-0100-00
正数三码合一, 所以结果为 16
*/
// 2. 计算 6 << 3
System.out.println("6 << 3 = "+(6 << 3)); // 6 << 3 = 48
/*
得到 6 的补码 0000-0000 0000-0000 0000-0000 0000-0110
左移三位 0-0000 0000-0000 0000-0000 0000-0110-000
正数三码合一, 所以结果为 48
*/
// 3. 计算 -7 << 2
/*
1. 得到 -7 的补码
-7 的源码 1000-0000 0000-0000 0000-0000 0000-0111
-7 的反码 1111-1111 1111-1111 1111-1111 1111-1000
-7 的补码 1111-1111 1111-1111 1111-1111 1111-1001
左移两位 11-1111 1111-1111 1111-1111 1111-1001-00 (结果的补码)
结果的反码 11-1111 1111-1111 1111-1111 1111-1000-11
结果的原码 10-0000 0000-0000 0000-0000 0000-0111-00
所以结果为 -28
*/
System.out.println("-7 << 2 = "+(-7 << 2)); // -7 << 2 = -28
System.out.println("3 << 3 = "+(3 << 3)); // 3 << 3 = 24
}
}
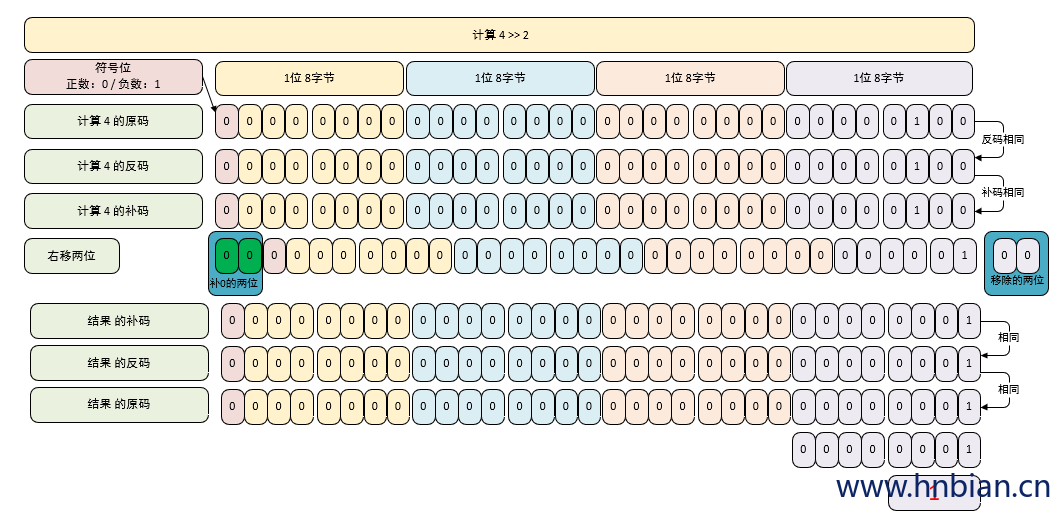
3.8 算术右移运算
- 算术右移是将二进制数整体右移指定位数,
- 如果操作数是 正数 右移后空出来的位用 0 补充
- 如果操作数是 负数 右移后空出来的位用 1 补充
- 操作符: >>
- 规律:$x >> n = x / ( 2^n )$
public class BitwiseRight {
public static void main(String[] args) {
// 1. 计算 4 >> 2
System.out.println("4 >> 2 = "+(4 >> 2));
// = 4 / (2^2) = 1
/*
得到 4 的补码 0000-0000 0000-0000 0000-0000 0000-0100
右移两位 00-0000-0000 0000-0000 0000-0000 0000-01
正数三码合一, 所以结果为 1
*/
// 2. 计算 6 >> 3
System.out.println("6 >> 3 = "+(6 >> 3)); // 6 >> 3 = 48
/*
得到 6 的补码 0000-0000 0000-0000 0000-0000 0000-0110
右移三位 000 0000-0000 0000-0000 0000-0000 0000-0
正数三码合一, 所以结果为 0
*/
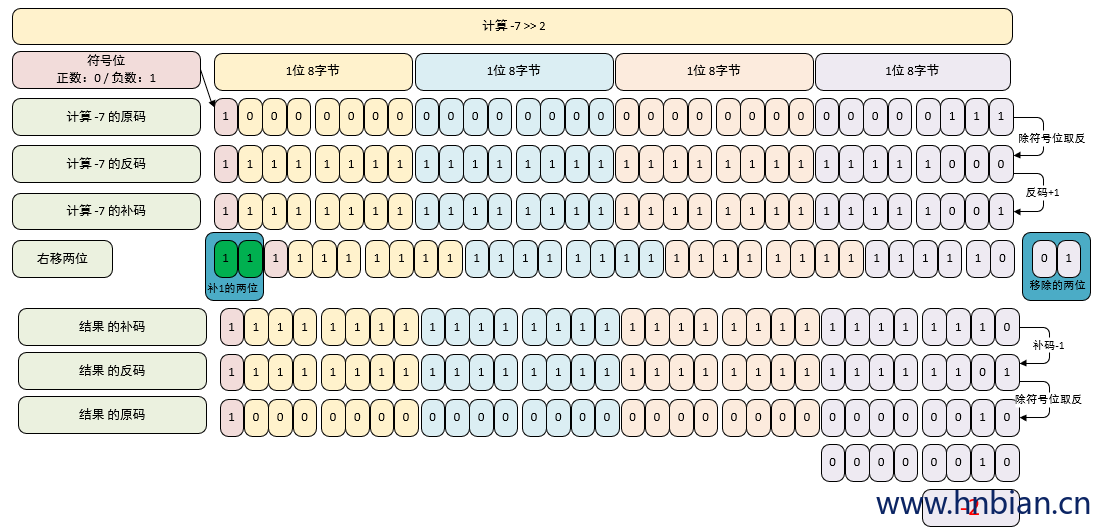
// 3. 计算 -7 >> 2
/*
1. 得到 -7 的补码
-7 的源码 1000-0000 0000-0000 0000-0000 0000-0111
-7 的反码 1111-1111 1111-1111 1111-1111 1111-1000
-7 的补码 1111-1111 1111-1111 1111-1111 1111-1001
右移两位 11-1111-1111 1111-1111 1111-1111 1111-10 (结果的补码)
结果的反码 11-1111-1111 1111-1111 1111-1111 1111-01
结果的原码 10-0000 0000-0000 0000-0000 0000-0000-10
所以结果为 -2
*/
System.out.println("-7 >> 2 = "+(-7 >> 2)); // -7 >> 2 = -2
System.out.println("-10 >> 2 = "+(-10 >> 2)); // -10 >> 2 = -3
System.out.println("-10 >> 3 = "+(-10 >> 3)); // -10 >> 3 = -2
System.out.println("-10 >> 4 = "+(-10 >> 4)); // -10 >> 4 = -1
System.out.println("3 >> 3 = "+(3 >> 3)); // 3 >> 3 = 0
}
}
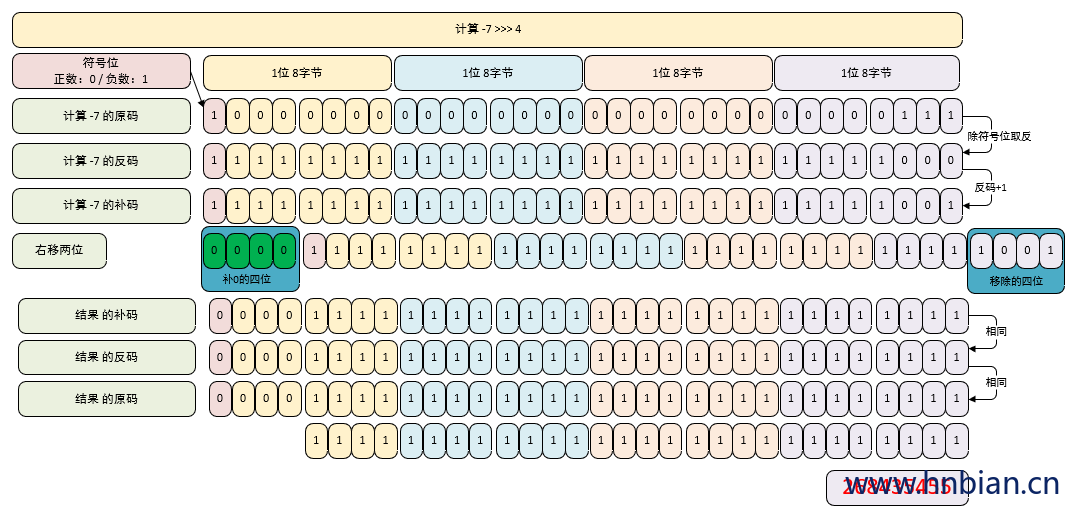
3.9 无符号右移运算
- 无符号右移是将二进制数整体右移指定位数, 右移后空出来的位用 0 补充
- 操作符: >>>
- 当操作数为正数的时候, 算术右移跟无符号右移相同位结果相同
- 无符号右移运算结果永远是正数
public class BitwiseRight2 {
public static void main(String[] args) {
// 1. 计算 4 >>> 2
System.out.println("4 >>> 2 = "+(4 >>> 2));
// = 4 / (2^2) = 1
/*
得到 4 的补码 0000-0000 0000-0000 0000-0000 0000-0100
右移两位 00-0000-0000 0000-0000 0000-0000 0000-01
正数三码合一, 所以结果为 1
*/
// 2. 计算 6 >>> 3
System.out.println("6 >>> 3 = "+(6 >>> 3)); // 6 >>> 3 = 48
/*
得到 6 的补码 0000-0000 0000-0000 0000-0000 0000-0110
右移三位 000-0000-0000 0000-0000 0000-0000 0000-0
正数三码合一, 所以结果为 0
*/
// 3. 计算 -7 >>> 4
/*
1. 得到 -7 的补码
-7 的源码 1000-0000 0000-0000 0000-0000 0000-0111
-7 的反码 1111-1111 1111-1111 1111-1111 1111-1000
-7 的补码 1111-1111 1111-1111 1111-1111 1111-1001
右移四位 0000-1111-1111 1111-1111 1111-1111 1111 (结果的补码)
正数三码合一, 所以结果为 268435455
*/
System.out.println("-7 >>> 4 = "+(-7 >>> 4)); // -7 >>> 2 = 268435455
System.out.println(0b1111111111111111111111111111); // 268435455
System.out.println("-10 >>> 2 = "+(-10 >>> 2)); // -10 >>> 2 = 1073741821
System.out.println("-10 >>> 3 = "+(-10 >>> 3)); // -10 >>> 3 = 536870910
System.out.println("-10 >>> 4 = "+(-10 >>> 4)); // -10 >>> 4 = 268435455
System.out.println("3 >>> 3 = "+(3 >>> 3)); // 3 >>> 3 = 0
}
}
4. 位运算的应用
4.1 判断奇偶数
只要根据数的最后一位是 0 还是 1 来决定即可,为 0 就是偶数,为 1 就是奇数。
int a = 10;
if(( a & 1 ) ==1){
System.out.println("奇数");
}else{
System.out.println("偶数");
}已知:
奇数最后一位为1
偶数最后一位为0
& 操作 同 1 为 1,其余为 0
所以:
任何奇数与 1 进行 & 操作结果都为 1
任何偶数与 1 进行 & 操作结果都为 0
4.2 交换数值
// 交换 a,b 的值
public static void swap(int a,int b){
System.out.println("交换前:a="+a+", b="+b);
a ^= b;
b ^= a;
a ^= b;
System.out.println("交换后:a="+a+", b="+b);
}- 异或操作规律
- 相同为 0 不同为 1
- 任何数与 0 做异或操作,结果都为其本身
- 任何数与本身做异或操作结果都为0
- 流程解析
a ^= b
同:a = ( a ^ b )
b ^= a
同:b = b ^ a
根据步骤1 得出 a = a ^ b
带入为:b = b ^ ( a ^ b )
简化为:b = b ^ a ^ b
简化为:b = b ^ b ^ a
已知: 任何数与本身做异或操作结果都为0
所以: b = 0 ^ a
已知: 任何数与 0 做异或操作,结果都为其本身
所以: b = a
a ^= b
同: a = a ^ b
根据步骤2得出: b = b ^ a
带入为:a = ( b ^ a ) ^ a
简化为:a = b ^ a ^ a
已知: 任何数与本身做异或操作结果都为0
所以:a = b ^ 0
已知: 任何数与 0 做异或操作,结果都为其本身
所以: a = b
- 使用位运算验证
a = 3; b = 5;
i1 = 3 的原码 0011
i2 = 5 的原码 0101
# 1. 计算 a ^= b;
0011
^ 0101
-----------
0110
# a = 0110 = 6
# 2. 计算 b ^= a;
0110
^ 0101
--------------
0011
# b = 0011 = 3
# 3. 计算 a ^= b;
0011
^ 0110
-------------
0101
# a = 0101 = 54.3 实现加法运算
4.3.1 原理介绍
用位运算实现加法, 也就是计算机用二进制进行位运算计算加法,
首先我们来实现用1位数的加法,这里暂时不考虑进位(满2进1)的情况。
# 1位2进制数,进行加法有四种情况, 即:
一位 二位 本位
1 + 1 = 0 # 这里为10,但是暂时不考虑进位,所以为0
1 + 0 = 1
0 + 1 = 1
0 + 0 = 0
# 可以用 异或运算符来代替
一位 二位 本位
1 ^ 1 = 0
1 ^ 0 = 1
0 ^ 1 = 1
0 ^ 0 = 0上面进行了一位运算,下面进行两位计算, 两位计算问题在于“进位”, 即满2进1 的问题,
一位 二位 进位
1 + 1 = 1 # 结果为10 , 这里只看进位为1
1 + 0 = 0
0 + 1 = 0
0 + 0 = 0
这里可以使用逻辑与操作符来代替
一位 二位 进位
1 & 1 = 1 # 进位 结果为10
1 & 0 = 0 # 不进位
0 & 1 = 0 # 不进位
0 & 0 = 0 # 不进位在位运算在中进位可以使用 逻辑左移运算符 “<<” 来实现,<< 1 也就是进1位
# 进位可以使用如下表达式
( a & b ) << 1到这里, 有了两个基本的表达式,即:
# 加法操作
a ^ b
# 进位操作
( a & b ) << 1做一下有两个位的2进制数的加法运算,在不考虑进位的情况下
# 1. 算数加法计算 11 + 01 = 100
11
+ 01
--------
100
# 2. 用推算的表达式计算 11 + 01
# 前面推算的表达式为:
# 1 ^ 1 = 0
# 1 ^ 0 = 1
# 0 ^ 1 = 1
# 0 ^ 0 = 0
# 2.1 首先计算 11 ^ 01
11 ^ 01 = 10
11
^ 01
--------
10
# 2.2 进位
(11 & 01) << 1 = 10
11
& 01
------------
01 << 1 # 左移一位
------------
10
# 到这里, 我们用普通的加法去运算两个数的时候可以得到 10 + 10 = 100
# 但是我们不需要加法,所以要想别的方法, 如果让两个数按照刚才的方法计算一次呢?
# 2.3 计算 10 ^ 10
10 ^ 10 = 00
10
^ 10
-----------
00
# 2.4 进位
(10 & 10) << 1 = 100
10
^ 10
-----------
10 << 1
-----------
100
#到这里就基本得出了结论,其实后面那个 00 已经不需要再去计算了, 因为第一个表达式就已经算出了结果, 通过推理可以得出三位数的加法只需要重复的计算三次,得到第一个表达式的值就是计算- 结论
设 a,b 为两个二进制数,则 a + b = a ^ b + ( a & b ) << 1
证明:a ^ b 时不考虑进位时加法结果。当二进制位同时为 1 时,才有进位,因此 ( a & b ) << 1 是进位产生的值,称为进位补偿。将两者相加便是完整加法结果。
使用 结论1 可以实现只用位运算进行加法运算。
证明:利用 结论1 中的 等式 不停对自身进行迭代。每迭代一次,进位补偿右边就多一位0,因此最多需要加数二进制位长度次迭代,进位补偿就变为0,这时运算结束。
4.3.2 代码实现与解析
- 通过代码使用位运算实现加法
public static void main(String[] args) {
add(11, 12);
}
private static int add(int a, int b) {
System.out.println("a = "+a+", b = "+b);
int sum = a;
while (b != 0) {
sum = a ^ b;
b = ( a & b ) << 1;
a = sum;
System.out.println("a= "+a+",b = "+b+", sum = "+sum);
}
System.out.println("结果 sum = "+sum);
return sum;
}
}
// 运算过程
a = 11 = 1011
b = 12 = 1100
1. 计算加法
sum = a ^ b
sum = 1011 ^ 1100
= 1011
^ 1100
--------
sum = 0111 = 7
2. 进位
b = (a & b) << 1
b = ( 1011 & 1100 ) << 1
1011
& 1100
----------------
1000 << 1
----------------
b = 10000 = 16
3. a = sum = 00111 = 7
4. b != 0 (true)
5. 计算加法
sum = a ^ b
sum = 00111 ^ 10000 = 10111
00111
^ 10000
--------------
sum = 10111 = 23
6. 进位
b = (a & b) << 1
b = ( 00111 & 10000 ) << 1
00111
& 10000
--------------
00000 << 1
--------------
b = 000000 = 0
7. a = sum = 10111
8. b != 0 (false) , 不进入循环,break;
9. 所以: sum = 10111 = 23
- 逻辑解析
add(5,3)
private static int add(int a, int b) {
System.out.println("a = "+a+", b = "+b);
int sum = a;
while (b != 0) {
// 做加法运算
sum = a ^ b;
// 进位
b = ( a & b ) << 1;
a = sum;
System.out.println("a= "+a+",b = "+b+", sum = "+sum);
}
System.out.println("结果 sum = "+sum);
return sum;
}
a = 5, b = 3
a= 6,b = 2, sum = 6
a= 4,b = 4, sum = 4
a= 0,b = 8, sum = 0
a= 8,b = 0, sum = 8
结果 sum = 8初始化数据 int a = 5; b = 3;
第一行: int sum = a;(int sum = 5)
第二行:while 循环 判断 b(3) !=0 为TRUE, 进入while 循环体
第三行(循环体第一行):sum = a ^ b(5 ^ 3)(计算加法1)
# 5 ^ 3 计算详情
# 5 = 0101(正数三码合一)
# 3 = 0011(正数三码合一)
0101
^ 0011
--------------
0110
# 所以: sum = 0110 (6)第四行(循环体第二行):b = ( a & b ) << 1; (5 & 3)<< 1 (进位1)
# (5 & 3)<< 1 计算详情
# 5 = 0101
# 3 = 0011
# 1. 计算 5 & 3
0101
& 0011
--------------
0001
# 2. 进行 算数左移
0001 << 1 = 0010
#所以:b = 0010 (2)第五行(循环体第三行): a = sum; (a= 0110 = 6)
第六行(循环体第四行):打印数据 a= 6, b = 2, sum = 6
第二行:while 循环 判断 b(2) !=0 为TRUE, 进入while 循环体
第三行(循环体第一行):sum = a ^ b(6 ^ 2)(计算加法2)
# 6 ^ 2 计算详情
# 6 = 0110(正数三码合一)
# 2 = 0010(正数三码合一)
0110
^ 0010
--------------
0100
# 所以: sum = 0100 (4)第四行(循环体第二行):b = ( a & b ) << 1; (6 & 2)<< 1 (进位2)
# (5 & 3)<< 1 计算详情
# 6 = 0110(正数三码合一)
# 2 = 0010(正数三码合一)
# 1. 计算 6 & 2
0110
& 0010
--------------
0010
# 2. 进行 算数左移
0010 << 1 = 0100
#所以:b = 0100 (4)第五行(循环体第三行): a = sum; (a= 0100 = 4)
第六行(循环体第四行):打印数据 a= 4, b = 4, sum = 4
第二行:while 循环 判断 b(4) !=0 为TRUE, 进入while 循环体
第三行(循环体第一行):sum = a ^ b(4 ^ 4)(计算加法3)
# 4 ^ 4 计算详情
# 4 = 0100(正数三码合一)
# 4 = 0100(正数三码合一)
0100
^ 0100
--------------
0000
# 所以: sum = 0000 (0)第四行(循环体第二行):b = ( a & b ) << 1; (4 & 4)<< 1 (进位3)
# (4 & 4)<< 1 计算详情
# 4 = 0100(正数三码合一)
# 4 = 0100(正数三码合一)
# 1. 计算 6 & 2
0100
& 0100
--------------
0100
# 2. 进行 算数左移
0100 << 1 = 1000
#所以:b = 1000 (4)第五行(循环体第三行): a = sum; (a= 0000 = 0)
第六行(循环体第四行):打印数据 a= 0, b = 8, sum = 0
第二行:while 循环 判断 b(8) !=0 为TRUE, 进入while 循环体
第三行(循环体第一行):sum = a ^ b(0 ^ 8)(计算加法4)
# 0 ^ 8 计算详情
# 0 = 0000(正数三码合一)
# 8 = 1000(正数三码合一)
0000
^ 1000
--------------
1000
# 所以: sum = 1000 (8)第四行(循环体第二行):b = ( a & b ) << 1; (0 & 8)<< 1(进位4)
# (4 & 4)<< 1 计算详情
# 0 = 0000(正数三码合一)
# 8 = 1000(正数三码合一)
# 1. 计算 6 & 2
0000
& 1000
--------------
0000
# 2. 进行 算数左移
0000 << 1 = 0000
#所以:b = 0000 (0)第五行(循环体第三行): a = sum; (a= 1000= 8)
第六行(循环体第四行):打印数据 a= 8, b = 0, sum = 8
第二行:while 循环 判断 b(0) !=0 为FALSE, 进入while 循环体
4.4 实现减法运算
已知 a - b = a + ( -b ) , 即取反后再用加法加起来即可
-b 即b 的相反数, 已知 ~X = -X-1 那么 ~X = (-X-1 )+1 即为 b 的相反数 即 ~X +1
public class BinaryMinus {
public static void main(String[] args) {
System.out.println(minus(10,-5));
}
/**
* 做减法操作
*
* @param a
* @param b
* @return
*/
private static int minus(int a, int b) {
return add(a, negative(b));
}
/**
* 求相反数
*
* @param num
* @return
*/
private static int negative(int num) {
return add(~num, 1);
}
/**
* 做加法操作
*
* @param a
* @param b
* @return
*/
private static int add(int a, int b) {
System.out.println("a = " + a + ", b = " + b);
int sum = a;
while (b != 0) {
sum = a ^ b;
b = (a & b) << 1;
a = sum;
System.out.println("a= " + a + ",b = " + b + ", sum = " + sum);
}
System.out.println("结果 sum = " + sum);
return sum;
}
}4.5 实现乘法运算
4.5.1 基本原理介绍
乘法的原理是通过加法计算,即a * b 就是将 b 个 a 相加。
我们先通过算数运算计算一下乘法运算 10 * 8
10 * 8 = 80
变换1 : (10*2) * (8/2) = 20 * 4 = 80
变换2 : (20*2) * (4/2) = 40 * 2 = 80
变换3 : (40*2) * (2/2) = 80 * 1 = 80这是最理想的情况,8 每次 除2 结果都是偶数,那当出现奇数的时候要怎么做呢?
10 * 6 = 60
变换1 = (10*2)*(6/2) = 20 * 3 = 60
变换2 = (20*2)*(3/2) = 40 * 1.5 = 60可是在计算机中, 当我们使用int类型数据做 相除运算 时 可不会得出 1.5 这样的浮点数
所以这一步我们得到的结果应该为
= ( 20 * 2 ) * ( 3 / 2 ) = 40 * 1 = 40这里的损失是1,即为前一步的20, 所以 40 + 20 = 60,
4.5.2 使用到的位运算符介绍
- 将算数逻辑梳理完成之后, 我们再看一下位运算中几个用到的运算符
- 算数左移(<<)
算数左移, 每移动一位相当于 乘 2 的操作, 例如:
System.out.println(4<<1); // 8
System.out.println(5<<1); // 10
System.out.println(10<<1); // 20- 无符号右移(>>>)
无符号右移每移动一位,相当于除以 2 ,例如:
System.out.println(4>>>1); // 2
System.out.println(8>>>1); // 4
System.out.println(10>>>1); // 5- 异或操作 (^)
乘法操作:当两个数均为正数或均为负数时, 结果为正数,当一个整数一个负数时,结果为负数
异或运算:异或运算与陈发运算类似, 当两个数的符号位相同时,进行异或操作符号位结果为0,即正数, 当符号位不一样时,结果为1,即负数
4.5.3 实现代码与解析
- 有了上面的介绍我们可以通过代码使用位运算实现乘法运算了
public class BinaryMulti {
public static void main(String[] args) {
System.out.println(multi(5,-6));
}
private static int multi(int a, int b) {
// 将乘数 和 被乘数都取绝对值
int multiplicand = a < 0 ? add(~a, 1) : a; // 被乘数
int multiplier = b < 0 ? add(~b, 1) : b; // 乘数
int res = 0;
// 判断 multiplier 任何数 * 0 = 0
while (multiplier != 0) {
//判断 multiplier 是不是 奇数
if ((multiplier & 1) != 0) {
// 如果是奇数 则加上一次multiplicand本身
res = add(res, multiplicand);
}
// multiplicand * 2
multiplicand <<= 1;
// multiplier / 2
multiplier >>>= 1;
}
// 计算乘积的符号
if ((a ^ b) < 0) {
res = add(~res, 1);
}
return res;
}
// 加法计算
private static int add(int a, int b) {
System.out.println("a = " + a + ", b = " + b);
int sum = a;
while (b != 0) {
sum = a ^ b;
b = (a & b) << 1;
a = sum;
System.out.println("a= " + a + ",b = " + b + ", sum = " + sum);
}
System.out.println("结果 sum = " + sum);
return sum;
}
}- 就是当 multiplier 是偶数时,则每次让 multiplicand * 2 直到 multiplier / 2 = 0时。
- 当b 是奇数时,先加上单独的那个 multiplicand,再重复 multiplier 为偶数的步骤。
- 过程解析
计算 10 * 5 ,结果很显然等于 50
设置 multiplicand=10, multiplier = 5
1. multiplier 不为0, 进入 while 循环
2. 判断 multiplier(5) 是奇数 则执行 res = add(res, multiplicand); res = 10;
3. multiplicand << 1 = 10 << 1 = 10 * 2 = 20;
4. multiplier >>> 1 = 5 << 1 = 5 / 2 = 2;
5. multiplier 不为0, 进入 while 循环
6. 判断 multiplier 不为0, 判断 multiplier(2) 是偶数, 不进入 if 执行体
7. multiplicand << 1 = 20 << 1 = 20 *2 = 40;
8. multiplier>>>1 = 2 >>> 1 = 2 / 2 = 1;
9. multiplier 不为0, 进入 while 循环
10. 判断 multiplier(1) 是奇数 则执行 res = add(res, multiplicand); res = 50;
11. multiplicand << 1 = 40 << 1 = 40 *2 = 80;
12. multiplier>>>1 = 1 >>> 1 = 1 / 2 = 0;
13. multiplier 为0, 不进入 while 循环, 循环结束, 结果 res 为 504.6 实现除法运算
实现除法运算有两种思路:
- 一种是使用减法运算
进行减法运算时, 不停的用除数减去被除数,知道除数小于被除数时,进行减法操作的次数就是商,此时被除数就是余数
这里还需要注意的就是商的符号,和余数的符号, 即他们是正数还是负数。商的符号确定方式跟乘法是一样的, 即除数被除数符号相同,则为正,如果除数与被除数符号不同,则为负,余数的符号和被除数的符号一致。计算流程和乘法类似, 我们需要先对两个数求绝对值,然后循环进行减法计算求商,然后求余数, 最后确定商与余数的符号。
- 一种是进行乘法运算
除法则可以视为乘法的逆运算。对于二进制来说,从高到低的每一位,将除数提升到当前位的权值(即,乘以2^k,等同于左移k位),如果此时被除数扔大于除数,就说明结果在这个位上商1。然后从被除数减掉除数提升后的值。遍历每一位,即为最终的结果。
public class BinaryDivide {
public static void main(String[] args) {
divideByMinus(20, 6);
divideByMulti(20, 6);
}
/**
* 通过乘法的方式实现除法
* @param a
* @param b
* @return
*/
public static void divideByMulti(int a, int b) {
// 对被除数和除数取绝对值
int A = a < 0 ? add(~a, 1) : a;
int B = b < 0 ? add(~b, 1) : b;
int N = 0; // 商 N
for (int i = 31; i >= 0; i--) {
// 未使用A>=(B<<i)进行判断,因为只有左移B时舍弃的高位不包含1,才相当于该数乘以2的i次方.
if ((A >> i) >= B) { // A ÷ 2^i >= B
N += (1 << i); // N = N + 2^i
A -= (B << i); // A = A - B*2^i
}
}
int C = A; // 余数C
// 求商的符号
if ((a ^ b) < 0) {
N = add(~N, 1);
}
// 求余数的符号
if (a < 0) {
C = add(~C, 1);
}
System.out.println("商是"+ N+", 余数 = "+ C);
}
/**
* 通过减法的方式实现除法
* @param a
* @param b
* @return
*/
public static void divideByMinus(int a, int b) {
//对被除数和除数取绝对值
int A = a < 0 ? add(~a, 1) : a;
int B = b < 0 ? add(~b, 1) : b;
//对被除数和除数的绝对值求商
int C = A; // 余数 C
int N = 0; // 商 N
while (C >= B) {
C = minus(C, B); // 余数, C-B
N = add(N, 1); // 计算次数 N+1
}
// 求商的符号
if ((a ^ b) < 0) {
N = add(~N, 1);
}
// 求余数的符合
if (a < 0) {
C = add(~C, 1);
}
System.out.println("商是"+ N+", 余数 = "+ C);
}
// 减法运算
private static int minus(int a, int b) {
return add(a, negative(b));
}
/**
* 求相反数
*
* @param num
* @return
*/
private static int negative(int num) {
return add(~num, 1);
}
// 加法运算
private static int add(int a, int b) {
//System.out.println("a = " + a + ", b = " + b);
int sum = a;
while (b != 0) {
sum = a ^ b;
b = (a & b) << 1;
a = sum;
//System.out.println("a= " + a + ",b = " + b + ", sum = " + sum);
}
//System.out.println("结果 sum = " + sum);
return sum;
}
}

![8.[Java 基础]流程控制结构](https://images.hnbian.cn/FrW2kxErcAXnSJuNQtxgfdcl60U3)
![6.[Java 基础]介绍运算符](http://images.hnbian.cn//Fk6-nPCYJD9c2IT5uFYVSuQRs5LH)